The Quantum Computing Research Group at Creighton University focuses on the theoretical, mathematical, and algorithmic aspects of quantum computing. Specifically, it investigates how the quantum version of a random walk, called a quantum walk, can be used to design efficient quantum algorithms.
The group is led by Prof. Tom Wong, and more information is available at his personal website, http://www.thomaswong.net.
Introduction to Quantum Walks
As an example of how different classical random walks and quantum walks can be, imagine person standing on the street. She flips a coin, and if it's heads, she takes a step to the left, and if it's tails, she takes a step to the right. After 100 steps, the probability of where she is is shown in the following graph:
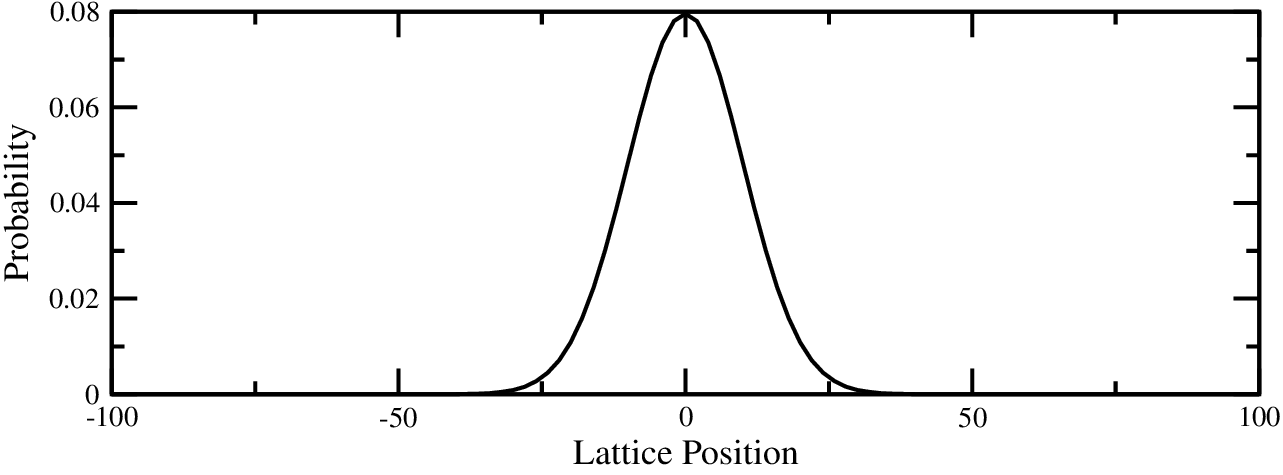
So in all likelihood, she hasn't strayed too far from her initial position at the middle.
Now say both the coin and the person are quantum. Now she makes a quantum coin flip, whose outcome is a complex linear combination of heads and tails. Then she steps to the left and right. After 100 steps, the resulting probability distribution looks much different:
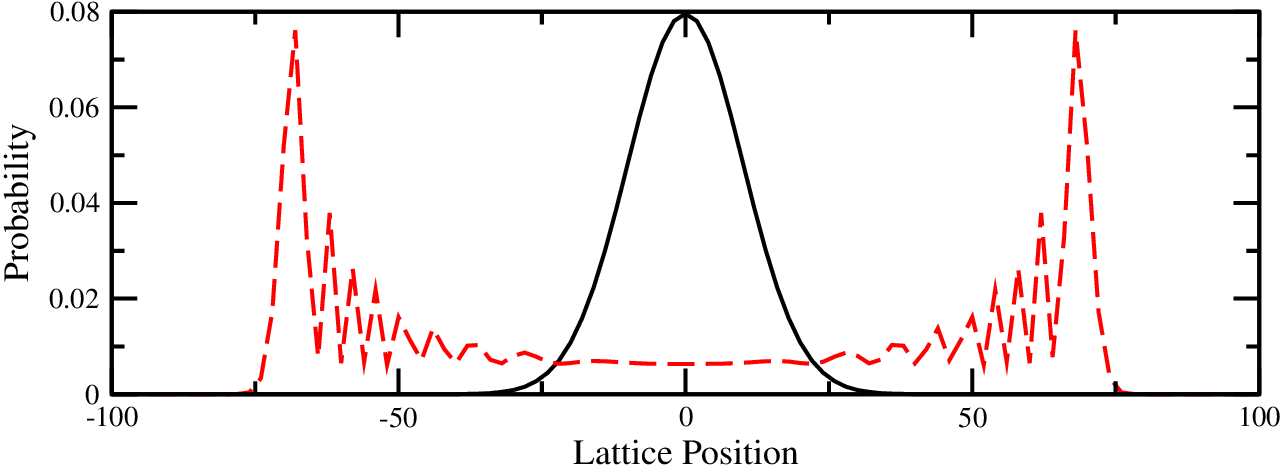
Now she has a substantial probability of being far away from her starting point. This indicates that quantum walks spread more quickly--quadratically more quickly, in fact.
Utilizing this behavior, quantum walks can be used to develop quantum algorithms that that outperform classical ones at a variety of tasks, such as searching, element distinctness, solving boolean formulas, finding triangles/clusters in networks, and more!
Mathematically, quantum walks are the usual equations of quantum physics--Schrödinger's equation and the Dirac equation--but in discrete space. In Schrödinger's equation, the kinetic term of the Hamiltonian is proportional to Laplace's operator. For a quantum walk, the discrete or graph version of Laplace's operator is used instead. In the Dirac equation, the spin of the particle is used as the coin of the quantum walk, which determines the direction in which the quantum walk hops.
Research Opportunities
Students with a strong background in physics, mathematics, and/or computer science are welcome to contact Dr. Wong about research opportunities. Note the Physics Department does not have a PhD program, but it does have a terminal master's program, and some teaching fellowships may be available that cover tuition, healthcare, and a modest stipend.